Phát hiện thấy 33 chủ đề phù hợp với toán hình 10 bài 3.




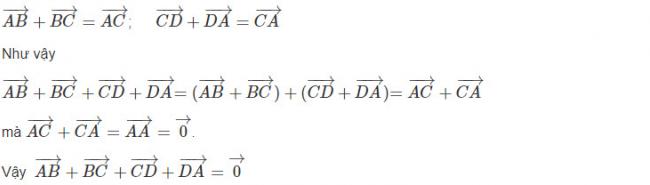








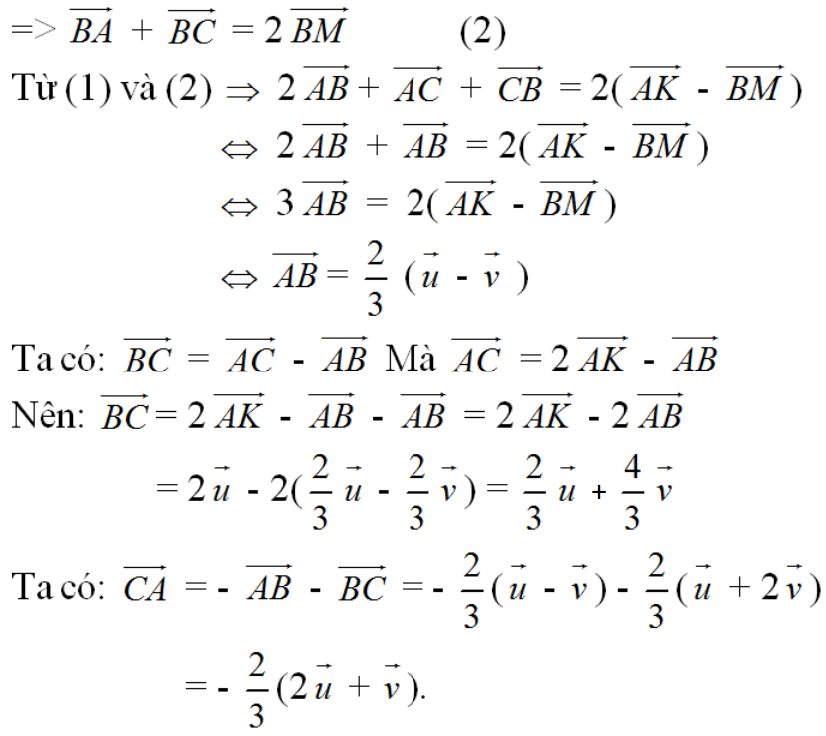



![Giải Toán 10] Chương 2: Tích vô hướng của hai vectơ và ứng dụng/ Bài 3: Các hệ thức lượng trong tam giác và giải tam giác Giải Toán 10] Chương 2: Tích Vô Hướng Của Hai Vectơ Và Ứng Dụng/ Bài 3: Các Hệ Thức Lượng Trong Tam Giác Và Giải Tam Giác](https://lop12.edu.vn/wp-content/uploads/2019/10/c23.png)






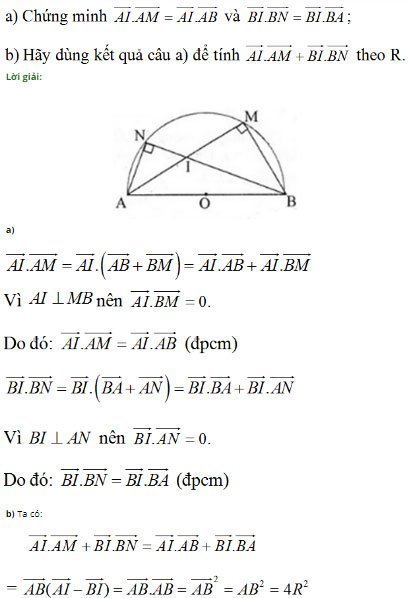





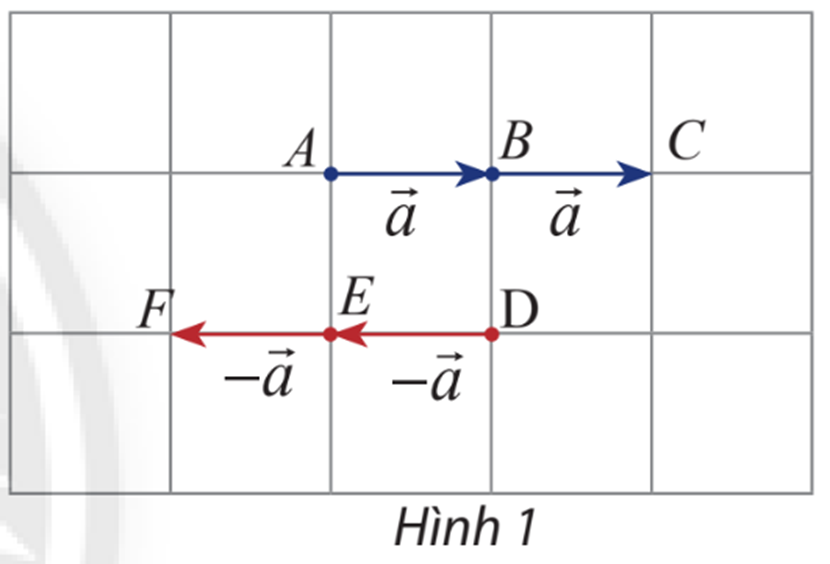



.png)






toán hình 10 bài 3
Lý thuyết về phương trình đường tròn
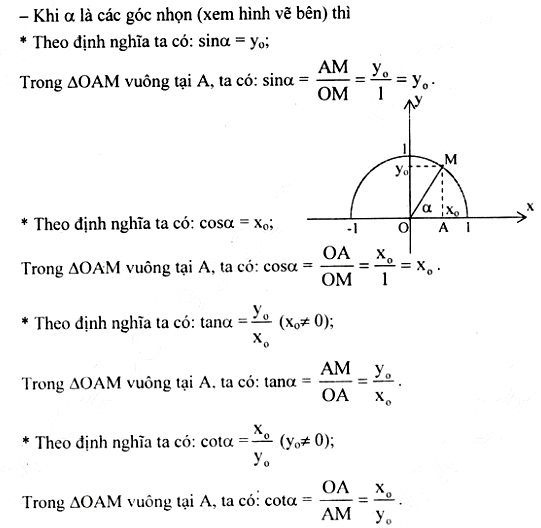
Phương trình đường tròn là một phương trình có dạng $(x-a)^2+(y-b)^2=r^2$, trong đó $(a,b)$ là tâm của đường tròn và $r$ là bán kính của đường tròn.
Bài tập về phương trình đường tròn
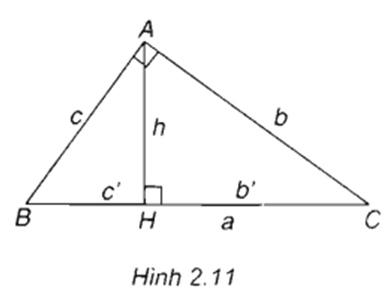
Có nhiều bài tập liên quan đến phương trình đường tròn trong Toán hình 10 bài 3. Ví dụ như bài tập tìm tọa độ tâm và bán kính của một đường tròn đã biết phương trình hoặc bài tập vẽ đường tròn khi biết tâm và bán kính. Để giải quyết những bài tập này, hãy chú ý đến cách sử dụng các công thức đơn giản như công thức khoảng cách và công thức tính bán kính.
Ứng dụng của phương trình đường tròn trong thực tế
Phương trình đường tròn được ứng dụng trong nhiều lĩnh vực khác nhau, từ khoa học đến kĩ thuật và thủ công. Ví dụ, trong định vị toàn cầu, vị trí của một vật được xác định bằng cách sử dụng nhiều đường tròn trong hệ thống GPS. Trong công nghệ, phương trình đường tròn được sử dụng để thiết kế các bộ phận chế tạo như đĩa CD hay tụ điện.
Cách giải quyết các vấn đề liên quan đến phương trình đường tròn
Để giải quyết các vấn đề liên quan đến phương trình đường tròn trong Toán hình 10 bài 3, chúng ta nên nắm vững lý thuyết về phương trình đường tròn và các công thức liên quan. Ngoài ra, cần phải tập trung vào khả năng áp dụng lý thuyết vào thực tế và sử dụng các bài tập để luyện tập kỹ năng.
FAQs:
1. Bài 3: Tích của một số với một vectơ là gì?
Bài 3 là một bài tập trong Toán hình 10 bài 3, trong đó ta cần tính tích của một số với một vectơ. Ví dụ, nếu biết vector $\vec{v}=(x_1,y_1)$ và số thực $k$, ta cần tính $\vec{u}=k\vec{v}=(kx_1,ky_1)$.
2. Các dạng bài tập tích của vectơ với một số có gì khác biệt?
Các dạng bài tập tích của vectơ với một số có thể khác nhau về cách tính hoặc cách sử dụng. Ví dụ, trong bài tập Tích của một số với một vectơ Chân trời sáng tạo, chúng ta cần tính tích của một số phức với một vectơ, trong khi đó trong bài tập Tích của một số với một vectơ – Cánh diều, ta cần tính tích của một số tự nhiên với một vectơ.
3. Làm sao để giải quyết các bài tập về phương trình đường tròn?
Để giải quyết các bài tập về phương trình đường tròn, chúng ta cần nắm vững lý thuyết về phương trình đường tròn và các công thức liên quan. Ngoài ra, cần phải tập trung vào khả năng áp dụng lý thuyết vào thực tế và sử dụng các bài tập để luyện tập kỹ năng.
Từ khoá người dùng tìm kiếm: toán hình 10 bài 3 Bài 3: Tích của một số với một vectơ, Toán 10 Bài 3: Tích của một số với một vectơ, Tích của một số với một vectơ Chân trời sáng tạo, Tích của một số với một vectơ – Cánh diều, Toán 10 Bài 3 Hình học chương 2, Bài 5: Tích của một số với một vectơ, Các dạng bài tập tích của vectơ với một số, Tích của một vectơ với một số Kết nối tri thức
Tag: Top 70 – toán hình 10 bài 3
Toán học lớp 10 – Chân trời sáng tạo – Chương 9 – Bài 3 – Đường tròn trong mặt phẳng toạ độ -Tiết 1
Xem thêm tại đây: buoitutrung.com
Link bài viết: toán hình 10 bài 3.
Xem thêm thông tin về chủ đề toán hình 10 bài 3.
- Gợi ý giải đáp chi tiết toán hình 10 bài 3 – Các hệ thức lượng …
- Giải SGK Toán 10 Bài 3 (Cánh diều): Khái niệm vectơ
- Giải Toán 10 Cánh diều Bài 3: Khái niệm vectơ
Categories: https://buoitutrung.com/img/