Có 18 chủ đề phù hợp với toán hình 12 bài 2.




















.png)












toán hình 12 bài 2
Phân tích đề bài và xác định các thông số cần tính:
Trước khi giải bài toán, việc phân tích đề bài và xác định các thông số cần tính là rất quan trọng. Các thông số cần tính thường được nêu trong đề bài, ví dụ như đường kính, bán kính của hình tròn, độ dài hai cạnh của hình chữ nhật, diện tích của hình vuông…
Áp dụng công thức tính diện tích và chu vi của hình:
Sau khi xác định các thông số cần tính, ta có thể áp dụng công thức tính diện tích và chu vi của hình tương ứng để tìm kết quả. Ví dụ, diện tích của hình tròn có bán kính R là: S = πR2. Chu vi của hình tròn là C = 2πR.
Giải quyết các bài toán liên quan đến hình tròn, tam giác, hình chữ nhật, hình vuông, tứ giác…
Toán hình 12 bài 2 cũng bao gồm giải quyết các bài toán liên quan đến hình tròn, tam giác, hình chữ nhật, hình vuông, tứ giác… Đối với từng loại hình, ta sử dụng các công thức và tính chất tương ứng để giải quyết bài tập.
Ví dụ, để tính cạnh của hình vuông khi biết diện tích, ta dùng công thức S = a2. Khi muốn tính đường cao của tam giác, ta có thể sử dụng công thức S = ½bh hoặc công thức của định lí Pythagoras.
Dùng tính chất và công thức của đường tròn ngoại tiếp, đường tròn nội tiếp để giải các bài tập
Đối với các bài toán liên quan đến hình tròn, ta còn có thể dùng tính chất và công thức của đường tròn ngoại tiếp, đường tròn nội tiếp để giải quyết các bài tập.
Đường tròn ngoại tiếp là đường tròn đi qua tất cả các đỉnh của hình đó. Đường tròn nội tiếp là đường tròn tiếp xúc với tất cả các cạnh của hình.
Ví dụ, để tính bán kính của đường tròn nội tiếp tam giác khi biết độ dài ba cạnh, ta dùng công thức: r = S/P, trong đó S là diện tích của tam giác, P là chu vi của tam giác.
FAQs
1. Toán hình 12 bài 2 là gì?
Toán hình 12 bài 2 là chương trình học tập trong môn Toán của học sinh cấp 3. Nội dung của bài toán bao gồm phân tích đề bài và xác định các thông số cần tính, áp dụng công thức tính diện tích và chu vi của hình, giải quyết các bài toán liên quan đến hình tròn, tam giác, hình chữ nhật, hình vuông, tứ giác…
2. Có những loại hình nào được giải quyết trong Toán hình 12 bài 2?
Trong Toán hình 12 bài 2, ta giải quyết các bài toán liên quan đến hình tròn, tam giác, hình chữ nhật, hình vuông, tứ giác… Với từng loại hình, ta sử dụng các công thức và tính chất tương ứng để giải quyết bài tập.
3. Làm sao để giải quyết các bài toán liên quan đến hình tròn?
Để giải quyết các bài toán liên quan đến hình tròn, ta sử dụng các công thức và tính chất của hình tròn, bao gồm bán kính, đường kính, diện tích và chu vi của hình tròn. Ta cũng có thể dùng tính chất và công thức của đường tròn ngoại tiếp, đường tròn nội tiếp để giải quyết các bài tập.
4. Làm sao để tính diện tích của hình?
Để tính diện tích của một hình, ta dùng công thức tương ứng với loại hình đó. Ví dụ, diện tích của hình tròn có bán kính R là: S = πR2. Diện tích của hình vuông có cạnh a là: S = a2.
5. Làm sao để tính chu vi của hình?
Để tính chu vi của một hình, ta dùng công thức tương ứng với loại hình đó. Ví dụ, chu vi của hình tròn là C = 2πR. Chu vi của hình chữ nhật có hai cạnh a và b là: C = 2(a + b).
Từ khoá người dùng tìm kiếm: toán hình 12 bài 2 toán hình 12 bài 2: phương trình mặt phẳng, Toán Hình 12 Bài 2: mặt cầu, Toán hình 12 bài 2 lý thuyết, Toán Hình 12 Bài 2 Chương 2, Toán hình 12 bài 2: mặt cầu lý thuyết, Toán Hình 12 Bài 2 chương 3, Toán Hình 12 bài 2 trang 80, Toán Hình 12 bài 2 trang 49
Tag: Update 28 – toán hình 12 bài 2
Phương trình mặt phẳng – Bài 2 – Toán học 12 – Thầy Trần Thế Mạnh (HAY NHẤT)
Xem thêm tại đây: buoitutrung.com
Link bài viết: toán hình 12 bài 2.
Xem thêm thông tin về chủ đề toán hình 12 bài 2.
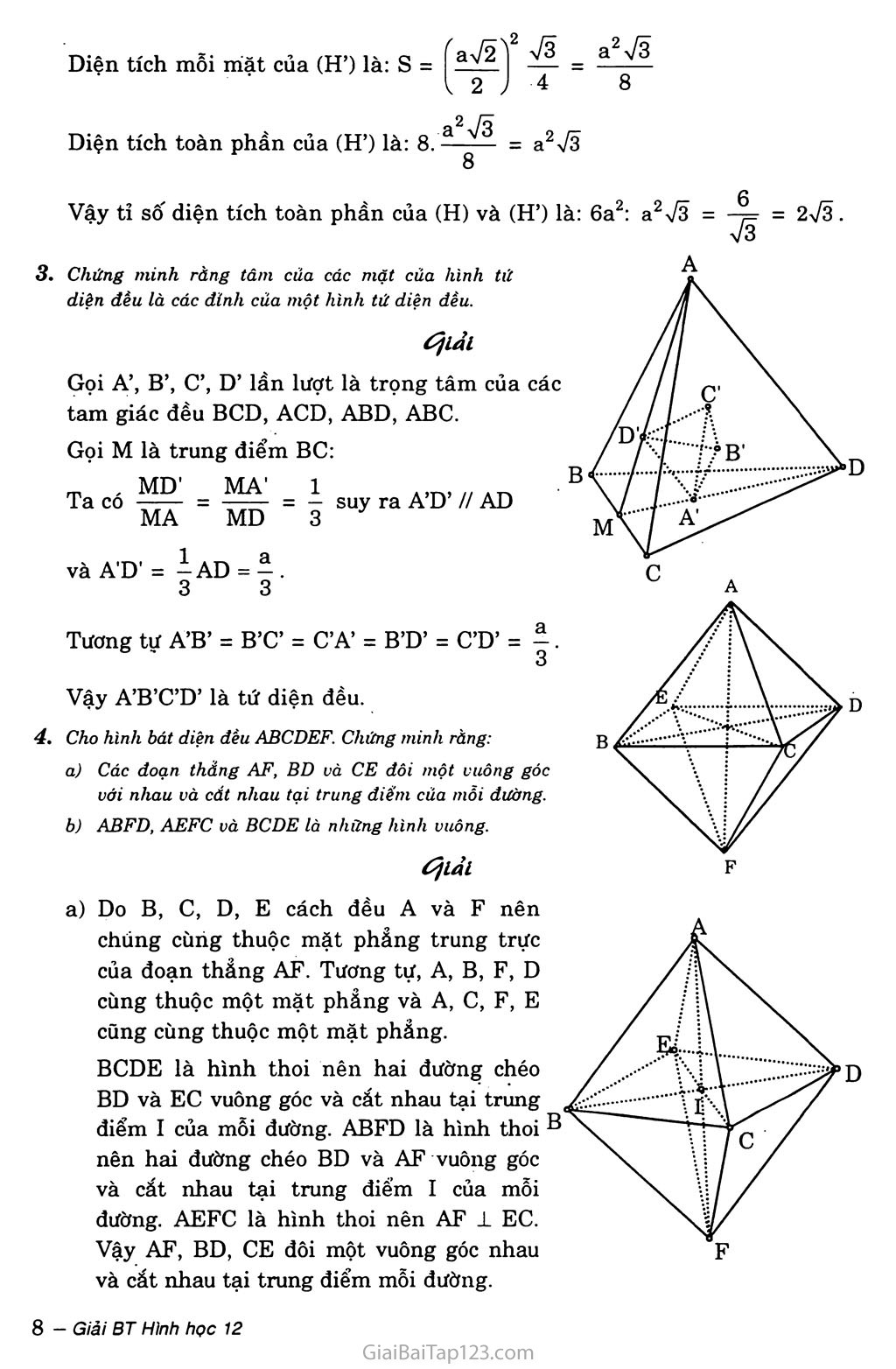
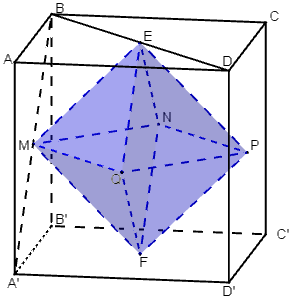
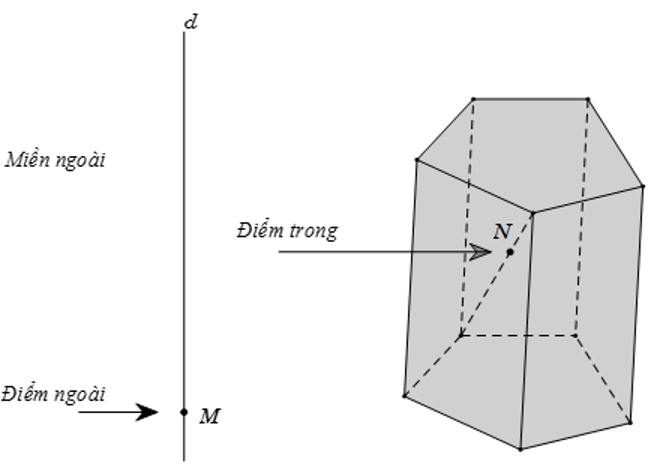
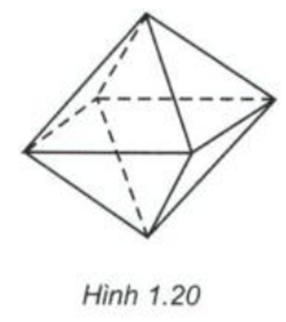
- Giải Toán 12 Bài 2: Khối đa diện lồi và khối đa diện đều
- Hình học 12 Bài 2: Khối đa diện lồi và khối đa diện đều
- Giải toán 12 Bài 2. Khối đa diện lồi và khối đa diện đều
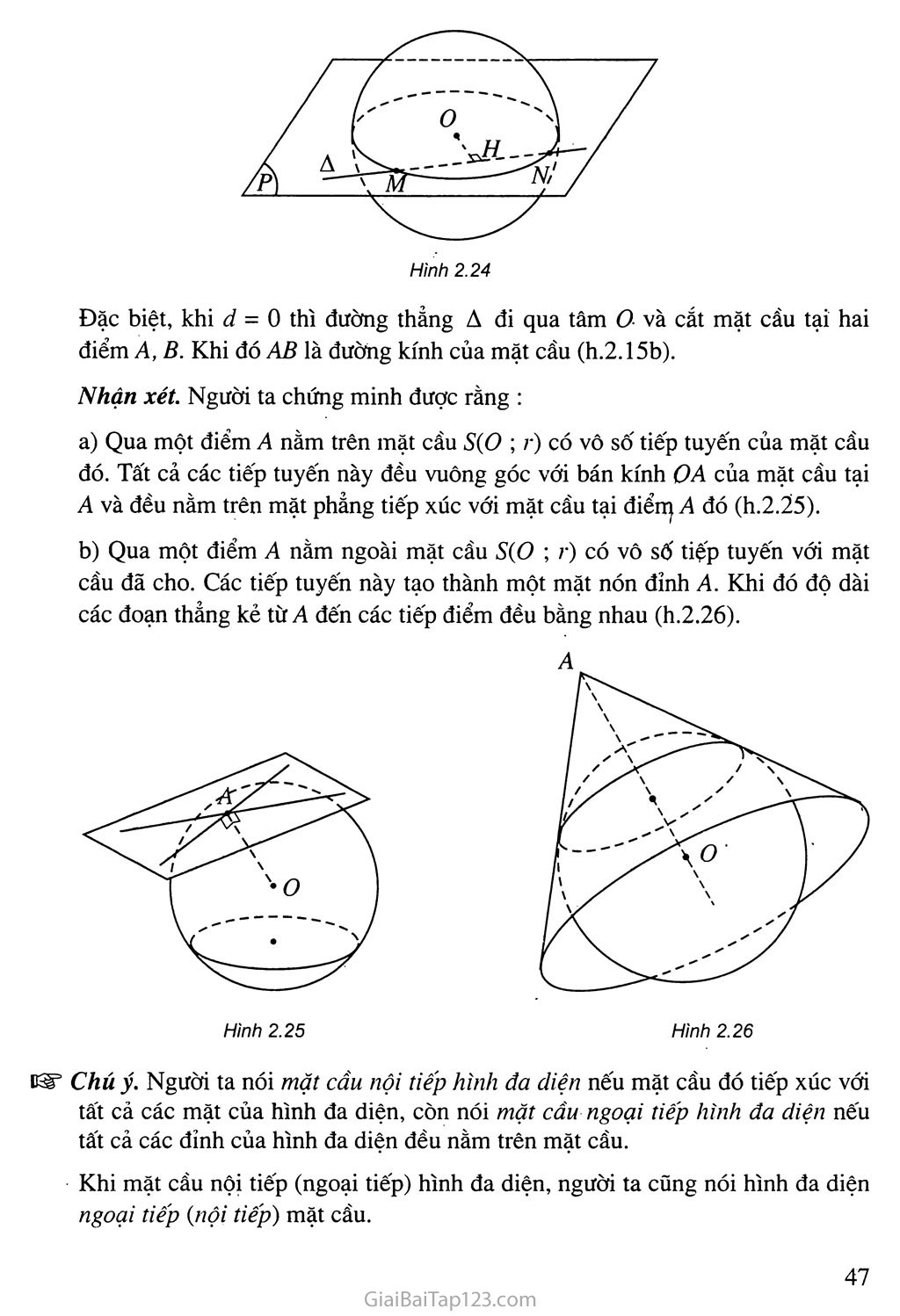
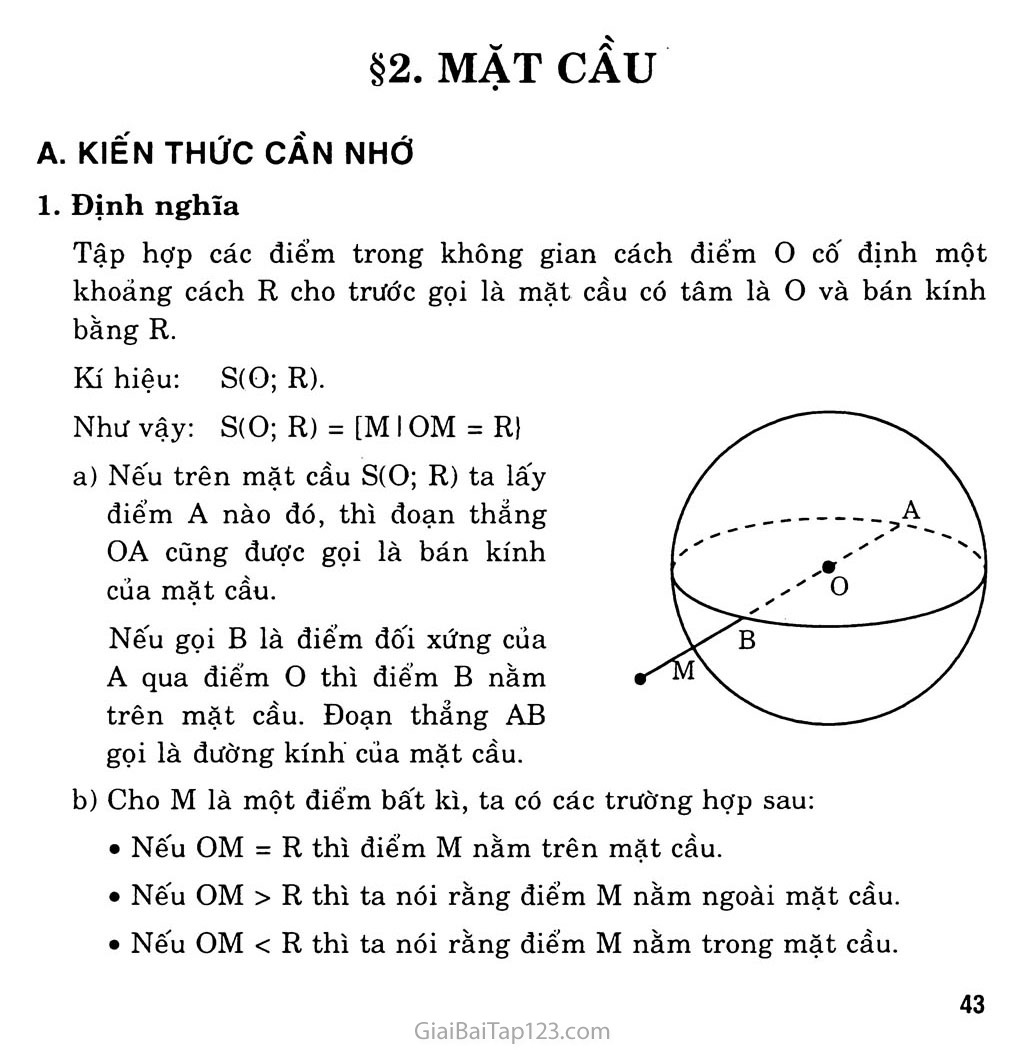
- Sách Giải Bài Tập Toán Lớp 12 Bài 2 : Mặt Cầu
- Giải Toán 12 Bài 2 : Mặt cầu
- SGK Hình học lớp 12 – Giải bài tập Bài 2: Khối đa diện lồi và …
Categories: https://buoitutrung.com/img/
