Hoe Een Breuk Delen Door Een Breuk: Een Eenvoudige Uitleg
Breuken – Delen Door Een Breuk (2 Havo/Vwo \U0026 2 Vwo)
Keywords searched by users: breuk delen door een breuk breuk delen door heel getal, ezelsbruggetje breuken delen, breuken delen voorbeeld, delen door een breuk is vermenigvuldigen met het omgekeerde, breuken delen oefeningen, breuken vermenigvuldigen, breuken delen groep 8, breuken delen rekenmachine
Breuk delen door een breuk: Een complete gids
Wat is een breuk?
Een breuk is een wiskundig concept dat wordt gebruikt om delen van een geheel of groep te vertegenwoordigen. Het bestaat uit twee delen: de teller en de noemer, gescheiden door een schuine streep. De teller geeft aan hoeveel delen er worden genomen, terwijl de noemer aangeeft in hoeveel gelijke delen het geheel is verdeeld.
Een breuk wordt geschreven in de vorm van A/B, waarbij A de teller is en B de noemer. Bijvoorbeeld, in de breuk 3/4 is 3 de teller en 4 de noemer. Dit betekent dat het geheel is verdeeld in 4 gelijke delen en we hebben er 3 van genomen.
Hoe deel je een breuk door een breuk?
Het delen van een breuk door een andere breuk klinkt misschien ingewikkeld, maar het kan eenvoudig worden gedaan door een paar eenvoudige stappen te volgen. Hier is een stapsgewijze handleiding om je te helpen:
Het omgekeerde van de tweede breuk nemen
Voordat we kunnen beginnen met delen, moeten we het omgekeerde van de tweede breuk nemen. Dit betekent dat we de teller en de noemer omwisselen. Bijvoorbeeld, als we 2/3 willen delen door 4/5, nemen we het omgekeerde van 4/5 en krijgen we 5/4.
Vermenigvuldigen met het omgekeerde
De volgende stap is om de eerste breuk te vermenigvuldigen met het omgekeerde van de tweede breuk. Ga door met het vermenigvuldigen van de tellers en de noemers. Bijvoorbeeld:
2/3 ÷ 4/5 = (2/3) * (5/4) = (2 * 5) / (3 * 4) = 10/12.
Vermenigvuldigen met een heel getal
Soms moet je een breuk delen door een heel getal. In dat geval kun je het hele getal eenvoudig vermenigvuldigen met de teller van de breuk. Bijvoorbeeld:
4 ÷ 2/3 = 4 * 3/2 = 12/2 = 6.
Optellen en aftrekken van breuken na het delen
In sommige gevallen moet je na het delen van breuken ook optellen of aftrekken. Dit kan worden gedaan door ervoor te zorgen dat de noemers gelijk zijn en vervolgens de tellers bij elkaar op te tellen of van elkaar af te trekken. Bijvoorbeeld:
1/3 ÷ 2/3 = (1/3) / (2/3) = (1/3) * (3/2) = 3/6 = 1/2.
Herleiden van breuken naar een vereenvoudigde vorm
Na het delen van breuken kan het nodig zijn om de breuk te herleiden naar de vereenvoudigde vorm. Dit betekent dat je de teller en de noemer door hetzelfde getal deelt om ze zo klein mogelijk te maken. Bijvoorbeeld:
6/12 = 1/2.
Voorbeelden en oefeningen
Om het delen van breuken beter te begrijpen, laten we een paar voorbeelden bekijken:
Voorbeeld 1: 1/2 ÷ 3/4
Stap 1: Neem het omgekeerde van 3/4, dus we krijgen 4/3.
Stap 2: Vermenigvuldig 1/2 met 4/3, dus we krijgen (1/2) * (4/3) = 4/6.
Stap 3: Vereenvoudig de breuk, dus 4/6 wordt 2/3.
Antwoord: 1/2 ÷ 3/4 = 2/3.
Voorbeeld 2: 3 ÷ 2/5
Stap 1: Vermenigvuldig 3 met 5/2, dus we krijgen (3) * (5/2) = 15/2.
Stap 2: Herleid de breuk naar de vereenvoudigde vorm, dus 15/2 wordt 7 1/2.
Antwoord: 3 ÷ 2/5 = 7 1/2.
Je kunt ook oefenen met het delen van breuken met behulp van verschillende oefeningen. Hier zijn een paar voorbeeldvragen:
Oefening 1: 2/3 ÷ 1/4
Oefening 2: 5/8 ÷ 3/5
Oefening 3: 1 ÷ 2/7
Waarom moet je breuken delen?
Er zijn verschillende situaties waarin het delen van breuken nodig is. Bijvoorbeeld:
– Bij het verdelen van voedsel of middelen onder een groep mensen in gelijke delen.
– Bij het berekenen van het deel van een geheel dat aan elk individu moet worden gegeven.
– In de financiële sector, bij het berekenen van rente of betalingen.
– In de wetenschap, bij het bepalen van de verhouding tussen stoffen in een chemische reactie.
Het delen van breuken is dus een nuttige vaardigheid in verschillende situaties om nauwkeurige berekeningen uit te voeren.
Decimale schrijfwijze van een breuk
De decimale schrijfwijze van een breuk is een andere manier om een breuk weer te geven. Het wordt vaak gebruikt bij het vergelijken van breuken of bij het werken met decimale getallen. Om een breuk naar een decimale vorm om te zetten, deel je de teller door de noemer. Bijvoorbeeld:
1/2 = 0,5
3/4 = 0,75
2/5 = 0,4
De decimale schrijfwijze van een breuk kan handig zijn in verschillende situaties, vooral bij het uitvoeren van complexere berekeningen.
Veelgestelde vragen
Wat is het ezelsbruggetje voor het delen van breuken?
Een handig ezelsbruggetje voor het delen van breuken is “delen door een breuk is vermenigvuldigen met het omgekeerde”. Dit betekent dat je de eerste breuk vermenigvuldigt met het omgekeerde van de tweede breuk om het resultaat te krijgen.
Kun je een voorbeeld geven van het delen van breuken?
Natuurlijk! Laten we 2/3 delen door 1/4 als voorbeeld nemen.
Stap 1: Neem het omgekeerde van 1/4, dus we krijgen 4/1.
Stap 2: Vermenigvuldig 2/3 met 4/1, dus we krijgen (2/3) * (4/1) = 8/3.
Stap 3: Vereenvoudig de breuk, dus 8/3 blijft als het antwoord.
Dus, 2/3 ÷ 1/4 = 8/3.
Zijn er oefeningen om het delen van breuken te oefenen?
Ja, er zijn verschillende oefeningen beschikbaar om het delen van breuken te oefenen. Je kunt online bronnen raadplegen zoals wiskundewebsites en -apps, of gebruikmaken van oefenboeken voor wiskunde. Door regelmatig te oefenen kun je je vaardigheden verbeteren en het delen van breuken beter onder de knie krijgen.
Zijn er calculator die breuken kunnen delen?
Ja, er zijn rekenmachines beschikbaar die het delen van breuken kunnen uitvoeren. Deze rekenmachines kunnen handig zijn als je snel en nauwkeurig breuken wilt delen zonder de stappen handmatig te doorlopen. Zorg ervoor dat je bekend bent met het gebruik van de rekenmachine en begrijpt hoe hij breuken deelt voordat je hem gebruikt.
Met deze uitgebreide gids heb je nu een stevige basis om breuken te delen door een breuk. Door de stappen te volgen en oefeningen uit te voeren, kun je je vaardigheden in het delen van breuken verbeteren en zelfvertrouwen krijgen in het uitvoeren van deze berekeningen. Breuken delen kan nuttig zijn in verschillende situaties, dus het is een waardevolle vaardigheid om te leren.
Categories: Details 93 Breuk Delen Door Een Breuk

Een breuk delen door een breuk is hetzelfde als de breuk vermenigvuldigen met het omgekeerde van de breuk.Twee breuken op elkaar delen is hetzelfde als de eerste breuk met het omgekeerde van de tweede breuk te vermenigvuldigen. De eerste stap is daarom om het omgekeerde van de tweede breuk te bepalen (waarbij de teller en de noemer van plaats gewisseld zijn). Daarna vermenigvuldig je de twee tellers.Stap 1. Delen door een breuk is vermenigvuldigen met het omgekeerde. Stap 2. Vermenigvuldig het hele getal met de teller.
Hoe Breuk Delen Door Een Breuk?
Wanneer je twee breuken door elkaar deelt, is het proces hetzelfde als het vermenigvuldigen van de eerste breuk met het omgekeerde van de tweede breuk. Om het omgekeerde van de tweede breuk te vinden, wissel je de teller en de noemer om. Vervolgens vermenigvuldig je de tellers van de twee breuken.
Hoe Moet Je Een Breuk Delen Door Een Heel Getal?
Hoe Moet Je Gedeeld Door Berekenen?
Wat Is De Deler Van Een Breuk?
Wat Is Een Tiendelige Breuk?
Details 31 breuk delen door een breuk



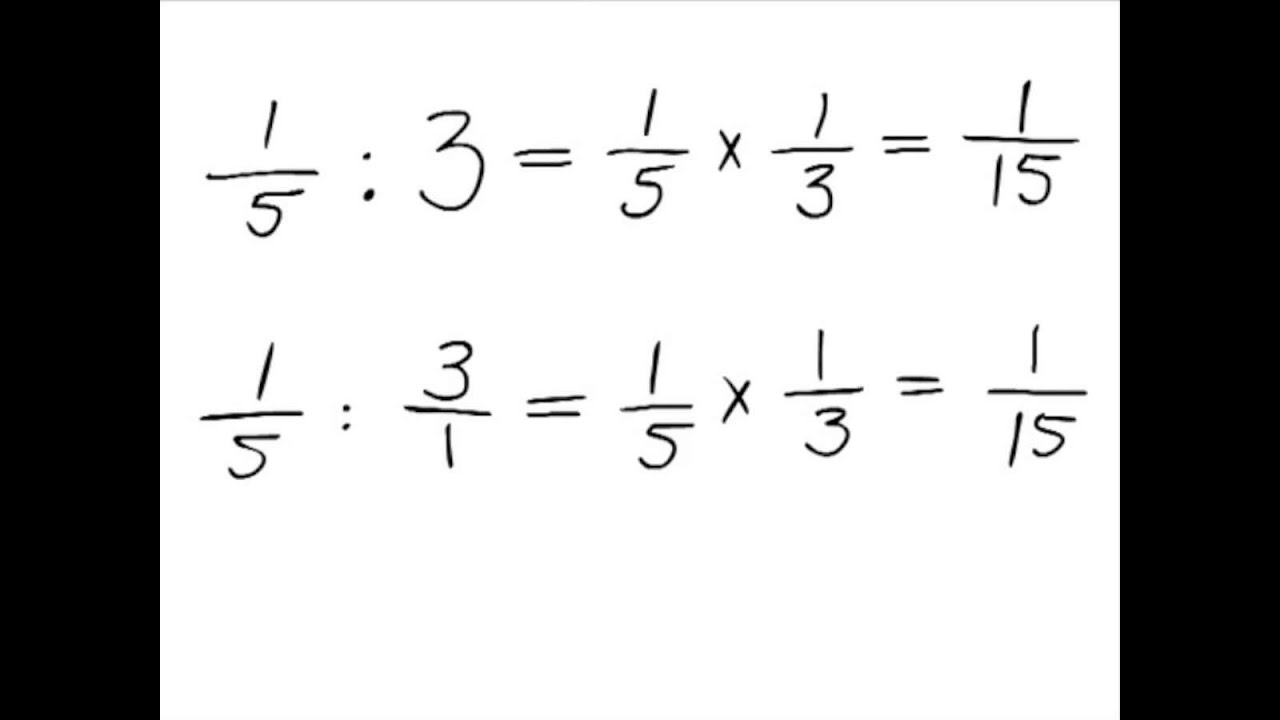


See more here: buoitutrung.com
Learn more about the topic breuk delen door een breuk.
- Breuken delen – Slimleren
- Breuken delen: 3/5 ÷ 1/2 (video) – Khan Academy
- Gevorderd – Heel getal delen door een breuk – Slimleren
- Vermenigvuldigen en delen – Slimleren
- 4 | Teller en noemer – Uitleg en oefenen met breuken
- Tiendelige breuk – Wikikids
See more: https://buoitutrung.com/business blog