สามเหลี่ยม สี่เหลี่ยม วงกลม
รูปเรขาคณิตถือเป็นหนึ่งในหัวข้อทางคณิตศาสตร์ที่สำคัญ ซึ่งมีลักษณะทางรูปทรงและคุณสมบัติที่น่าสนใจอย่างมาก โดยเฉพาะสามเหลี่ยม สี่เหลี่ยม และวงกลม ในบทความนี้เราจะมาสำรวจและเรียนรู้เพิ่มเติมเกี่ยวกับทั้งสามรูปเรขาคณิตที่ท้าทายอยู่ในชีวิตประจำวันของเรา
สามเหลี่ยม:
1. ลักษณะทางรูปทรงและคุณสมบัติพื้นฐานของสามเหลี่ยม
สามเหลี่ยมเป็นรูปเรขาคณิตที่ประกอบด้วยด้านสามด้านที่เชื่อมต่อกัน โดยการเชื่อมต่อด้วยเส้นตรง รูปร่างของสามเหลี่ยมเป็นตัวอย่างของความสมมาตร และมีลักษณะเฉพาะต่างๆ ซึ่งประกอบไปด้วยสามเหลี่ยมมุมแหลม สามเหลี่ยมมุมฉาก และสามเหลี่ยมมุมป้านฉาก
2. การหาความยาวและพื้นที่ของสามเหลี่ยม
เพื่อหาความยาวของด้านและหาพื้นที่ของสามเหลี่ยม สามารถใช้สูตรต่อไปนี้ได้:
– สูตรพิพากษา: ในกรณีที่ทราบความยาวของด้านสามด้าน แต่ยังไม่ทราบพื้นที่ สามารถใช้สูตรปริซึมได้ สูตรหนึ่งที่ใช้บ่อยคือ สูตรเฮอรอน
เส้นรอบวง (P) = a + b + c
พื้นที่ (A) = \sqrt{s(s-a)(s-b)(s-c)} โดยที่ s คือครึ่งหนึ่งของเส้นรอบวงและ a, b, c คือ ความยาวของด้านสามเหลี่ยม
– สูตรอื่นๆ: สำหรับกรณีที่ทราบความยาวของด้านสามเหลี่ยมทั้งสามด้าน สามารถใช้สูตรพื้นที่ของสามเหลี่ยมทั่วไป ซึ่งก็คือ A = \frac{1}{2} \times b \times h โดยที่ b คือความยาวของด้านฐาน และ h คือความสูงของสามเหลี่ยมจากด้านฐาน
3. ลักษณะเฉพาะของสามเหลี่ยมกลางและสามเหลี่ยมมุมฉาก
– สามเหลี่ยมกลาง: เป็นสามเหลี่ยมที่มีเส้นตรงที่ตัดกลางแกนของด้านสามเหลี่ยม ทำให้มีความยาวของด้านทั้งสี่เท่ากัน
– สามเหลี่ยมมุมฉาก: เป็นสามเหลี่ยมที่มีมุมฉากหนึ่ง กล่าวคือมีมุมป้านในสามเหลี่ยมที่มีมากกว่า 90 องศา
4. หลักการแบ่งสามเหลี่ยมตามเหลี่ยมด้าน
สามเหลี่ยมสามารถแบ่งออกเป็นหลายรูปแบบตามความยาวของด้าน โดยปกติแล้วมีหลักการแบ่งดังนี้:
– สามเหลี่ยมด้านเท่า: คือสามเหลี่ยมที่มีด้านทั้งสามมีความยาวเท่ากัน
– สามเหลี่ยมด้านไม่เท่า: คือสามเหลี่ยมที่มีด้านสองด้านที่มีความยาวเท่ากัน และด้านที่สามมีความยาวแตกต่างจากด้านสองด้านนั้น
– สามเหลี่ยมสมบูรณ์: คือสามเหลี่ยมที่มีด้านทั้งสามมีความยาวไม่เท่ากัน
5. สูตรคำนวณเส้นรอบวงและพื้นที่ของสามเหลี่ยม
สามเหลี่ยมสามารถคำนวณเส้นรอบวงและพื้นที่ได้ด้วยสูตรต่อไปนี้:
– เส้นรอบวง (P) = a + b + c
– พื้นที่ (A) = \sqrt{s(s-a)(s-b)(s-c)} โดยที่ s = \frac{P}{2} และ a, b, c คือ ความยาวของด้านสามเหลี่ยม
6. ความสัมพันธ์ระหว่างสามเหลี่ยมกับรูปทรงอื่น
สามเหลี่ยมเป็นรูปเรขาคณิตที่ใช้งานและเชื่อมโยงกับหลายรูปแบบอื่นๆ ตัวอย่างเช่น:
– สามเหลี่ยมกลางจะเป็นพื้นที่รอบวงของสามเหลี่ยม
– สามเหลี่ยมมุมฉากสามารถแบ่งเป็นสองสามเหลี่ยมมุมป้านฉาก
– สามเหลี่ยมสามารถแปลงเป็นสี่เหลี่ยมได้โดยการเพิ่มด้านเส้นตรงหนึ่ง
7. วิธีการใช้ประโยชน์ของสามเหลี่ยมในชีวิตประจำวัน
สามเหลี่ยมเป็นรูปเรขาคณิตที่พบในชีวิตประจำวันของเราในหลายๆ ด้าน เช่น:
– กราฟิกและการออกแบบ: รูปร่างสามเหลี่ยมถูกใช้ในการสร้างกราฟิก โลโก้ และการออกแบบสินค้า เพื่อให้ดูมีความสมดุลและสมส่วน
– การทำธุรกรรมทางเส้นตรง: ความหมายและความสัมพันธ์ระหว่างสามเหลี่ยมมีความสำคัญในตัวตนทางธุรกิจเช่น คำนวณรายได้ การคำนวณเส้นทาง และการวางแผนธุรกิจ
– ในเทคโนโลยี: การนำสามเหลี่ยมมาประยุกต์ใช้ในโครงสร้างเครือข่าย แบบสามเหลี่ยมช่วยให้สามารถเข้าถึงอุปกรณ์ในระยะไกลได้ตลอดเวลา
สี่เหลี่ยม:
1. ลักษณะทางรูปทรงและคุณสมบัติพื้นฐานของสี่เหลี่ยม
สี่เหลี่ยมเป็นรูปเรขาคณิตที่ประกอบด้วยสี่ด้านที่เชื่อมต่อกัน โดยเส้นตรง ทรงรูปของสี่เหลี่ยมมีลักษณะเ
รถไฟบ๊อบ – ผจญภัยกับรูปร่างต่างๆ | Bob The Train – Adventure With Shapes
คำสำคัญที่ผู้ใช้ค้นหา: สามเหลี่ยม สี่เหลี่ยม วงกลม รูปเรขาคณิต, รูปภาพวงกลม, สามเหลี่ยมภาษาอังกฤษ, สัญลักษณ์สามเหลี่ยม, Squid Game รีวิว, Squid Game คือ
รูปภาพที่เกี่ยวข้องกับหัวข้อ สามเหลี่ยม สี่เหลี่ยม วงกลม

หมวดหมู่: Top 96 สามเหลี่ยม สี่เหลี่ยม วงกลม
ดูเพิ่มเติมที่นี่: buoitutrung.com
รูปเรขาคณิต
รูปเรขาคณิต (Geometry) เป็นสาขาหนึ่งของคณิตศาสตร์ที่ศึกษาเกี่ยวกับรูปร่างและสมการเชิงกายภาพของวัตถุ โดยเน้นการศึกษาเกี่ยวกับทรงกลม สามเหลี่ยม สี่เหลี่ยม เรขาคณิตโคลนิก รูปรี และรูปพีระมิดอื่น ๆ ที่เราพบเห็นในชีวิตประจำวัน รูปเรขาคณิตเป็นสิ่งที่มีอยู่ร่วมกับเราตลอดเวลา ไม่ว่าจะเป็นในธรรมชาติหรือมนุษย์ก็ตาม เราจึงสามารถรู้จักและศึกษารูปร่างและคุณสมบัติต่าง ๆ ของวัตถุได้อย่างละเอียดอ่อน ซึ่งรูปเรขาคณิตเป็นสิ่งสำคัญที่มีบทบาทในการพัฒนาวิทยาศาสตร์ วิศวกรรม และศิลปะในอดีตและปัจจุบัน
ประวัติความเป็นมาของรูปเรขาคณิต
รูปเรขาคณิตเป็นสิ่งที่มีอยู่ตั้งแต่สมัยโบราณ อดีตมนุษย์ใช้รูปเรขาคณิตในการแบ่งแยกพื้นที่พอเหมาะกับการเก็บเกี่ยวผลผลิต ในสมัยแระแห่งมรดกวัตถุมงคลอียิปต์ รูปสามเหลี่ยมและรูปสี่เหลี่ยมถูกบูรณาการในการสร้างพิราบ และภายหลังก็นำมาใช้ในการวางแผนการก่อสร้างวัดและอนุสาวรีย์ในสมัยกรีก และโรมัน ในศตวรรษที่ 3 และที่ 4 กลไกการเดินเรือของคนกรีกคือโดยอ้างอิงเพียงแค่รูปเรขาคณิต
ในสมัยกลาง ทศวรรษที่ 16 เกิดการค้นพบการงดงามในความสัมพันธ์ระหว่างรูปร่างต่าง ๆ และความขัดแย้งเชิงคณิตศาสตร์ระหว่างโบราณกรรมและความรู้คณิตศาสตร์ พี่น้องแม่ข่ายหายากของคนคอปเปอร์นิกัสได้สร้างขึ้นในตอนปลายของยุคศตวรรษที่ 16 และช่วงหลัง แม้จะแสดงความคิดที่เหลือเชื่อในสภาพที่เป็นที่แน่นอนและเสถียรและสิ่งแวดล้อมอาจมีผลต่อสามารถของพี่น้องแม่ข่ายในระดับเบื้องต้น การศึกษาแต่ละส่วนคอปเปอร์นิกัสเราจำเป็นต้องการบทศาสตร์วิภาคศาสตร์อากัประสิทธิ์การเคลื่อนที่ของสิ่งของอย่างน้อย
ความสำคัญของรูปเรขาคณิต
รูปเรขาคณิตมีความสำคัญอย่างมากในหลายด้านของชีวิตประจำวัน รูปเรขาคณิตมอบให้เราความเข้าใจในการเดินทาง เช่น เมื่อเราเดินทางเราใช้เรขาคณิตเพื่อหาทิศทาง เช่น เมื่อเรามีความจำเป็นต้องใช้เทคโนโลยีไอทีเราก็สามารถใช้ความรู้จากรูปเรขาคณิตในการแก้ไขปัญหาดังกล่าวได้
นอกจากนี้รูปเรขาคณิตยังมีบทบาทสำคัญในสาขาต่าง ๆ ของวิทยาศาสตร์และวิศวกรรมเช่น ฟิสิกส์ ทฤษฎีผลิตภาพการรักษาสิ่งแวดล้อม การวิเคราะห์ข้อมูล การสร้างที่อยู่อาศัยที่ปลอดภัย และอื่น ๆ นอกจากนี้ รูปเรขาคณิตยังเป็นหนึ่งในวิชาอาหรับสมัยหลังพัฒนาซึ่งอยู่เบื้องหน้าในการคิดหาระยะห่างระหว่างของจักรวาลและสิ่งก่อสร้างของธรรมชาติ รูปเรขาคณิตยังมีบทบาทในวิชาศิลปะเช่นวัฒนธรรมแอฟริกันโมร็อคโกและศิลปะตะวันออกกลางเป็นต้น
คำถามที่พบบ่อย
1. รูปเรขาคณิตมีบทบาทอย่างไรในชีวิตประจำวัน?
รูปเรขาคณิตมอบความเข้าใจในการเดินทางและการใช้เทคโนโลยี นอกจากนี้ยังมีบทบาทในวิทยาศาสตร์ ศิลปะ และวิศวกรรม
2. รูปเรขาคณิตมีความสำคัญในศิลปะอย่างไร?
รูปเรขาคณิตมีบทบาทในวิชาศิลปะเช่นวิธีการเขียน การสร้างและความเจริญของศิลปะต่าง ๆ
3. ทำไมความรู้ในรูปเรขาคณิตถึงสำคัญสำหรับวิทยาศาสตร์และวิศวกรรม?
ความรู้ในรูปเรขาคณิตเป็นพื้นฐานสำหรับการพัฒนาองค์ความรู้ในวิทยาศาสตร์และวิศวกรรม เช่น การคำนวณพื้นที่ การวิเคราะห์ข้อมูล และการสร้างสิ่งประดิษฐ์
4. รูปเรขาคณิตมีบทบาทในการสร้างที่อยู่อาศัยที่ปลอดภัยอย่างไร?
รูปเรขาคณิตมีบทบาทในการออกแบบและกำหนดขนาดของสิ่งก่อสร้างเพื่อให้เหมาะสมและปลอดภัย ลักษณะเรขาคณิตของบริเวณและวัสดุสามารถกำหนดคุณสมบัติทางกายภาพและผลของแรงก่อนและหลังการกำจัด
5. สามารถใช้รูปเรขาคณิตในการวางแผนทางธุรกิจได้อย่างไร?
รูปเรขาคณิตสามารถใช้ในการวางแผนทางธุรกิจได้โดยการใช้เทคนิคการวางแผนเชิงการลงทุน การจัดทำแผนที่ระบบลูกน้ำ และการวางแผนการส่งมอบสินค้าเพื่อมุ่งเน้นความปลอดภัยและประสิทธิภาพ
6. มีรูปเรขาคณิตอย่างไรในวัฒนธรรมและภาษาของเรา?
รูปเรขาคณิตมีบทบาทในสถาปัตยกรรม คณิตศาสตร์กรีก และภาษาวรรณคดีตะวันตกและตะวันออกกลาง เช่น พีระมิดและพระองค์สีสามเหลี่ยมในวรรณคดียูริปิดีเยะ
รูปภาพวงกลม
รูปภาพวงกลมเป็นสัญลักษณ์ที่คุ้นเคยและเห็นตั้งแต่เรียนจดบันทึกรูปลงในพาร์ทโนจักรแรก รูปภาพวงกลมมีความสำคัญมากในด้านทฤษฎีทางคณิตศาสตร์และกราฟิกดีไซน์ นอกจากนี้ รูปภาพวงกลมยังเป็นสัญลักษณ์ที่ไว้ใจได้ในชีวิตประจำวันอย่างง่ายดาย ในบทความนี้เราจะสำรวจความสำคัญและการใช้งานของรูปภาพวงกลมในชีวิตประจำวัน เริ่มต้นจากกรรมวิธีกับการคำนวณบริเวณของวงกลมไปจนถึงการนำมาใช้ในชีวิตประจำวันต่าง ๆ
ความสำคัญของรูปภาพวงกลมในทางทฤษฎีทางคณิตศาสตร์เริ่มที่การคำนวณบริเวณของวงกลม สูตรที่ใช้คำนวณบริเวณของวงกลมคือ π r^2 ซึ่ง π (พาย) เป็นค่าคงที่ที่ใช้กรณีบริสุทธิ์และมีค่าประมาณเท่ากับ 3.14 ส่วน r (รัศมี) คือระยะทางจากศูนย์กลางของวงกลมไปยังจุดบนวงกลม หรือระยะทางรอบวงกลมหารด้วย 2 ณ ศูนย์กลางของวงกลม นอกจากนี้ยังมีความสำคัญของจำนวนพีระมิดเดลที่เกี่ยวข้องกับรูปภาพวงกลมซึ่งมีค่าเท่ากับ 2πR โดยที่ R คือรัศมีของวงกลม
รูปภาพวงกลมยังมีการใช้งานในด้านกราฟิกดีไซน์ โดยเฉพาะอย่างยิ่งในการออกแบบโลโก้ รูปภาพวงกลมเป็นที่นิยมสำหรับการออกแบบกราฟิกเนตรนารี และการออกแบบโลโก้กลุ่มนักร้ายต่าง ๆ เนื่องจากวงกลมมีความเป็นสัญลักษณ์แบบผู่ผวาที่แปลได้หลายความหมาย เช่น มีความเพื่อสันติภาพ ความเสมอภาค ความรอบคอบ เป็นต้น รูปภาพวงกลมยังสามารถใช้งานในการสร้างรูปภาพที่สวยงาม ดูดีต่อตาผู้ชม และสะดวกต่อการเรียนรู้
นอกจากความสำคัญในทางทฤษฎีทางคณิตศาสตร์และกราฟิกดีไซน์แล้ว รูปภาพวงกลมยังมีความสำคัญและการใช้งานในชีวิตประจำวันของเราด้วย อย่างเช่นในการวาดและเขียน การวาดวงกลมที่สวยงามและแขนง สามารถช่วยให้คุณแสดงออกอารมณ์ที่ต้องการได้อย่างละเอียดอ่อนได้อย่างดี การวาดวงกลมยังเป็นเรื่องสนุกสนานสำหรับเด็ก ๆ ซึ่งช่วยพัฒนาทักษะทางการสื่อสารและความคิดสร้างสรรค์
นอกจากนี้ รูปภาพวงกลมยังมีอีกหน้าที่หลายอย่างเช่นในการทำอาหาร รูปภาพวงกลมมักถูกนำมาใช้ในการกลบกลิ่น หรือใช้ในการตัดเค้กตกแต่ง เพราะรูปภาพวงกลมสามารถให้พื้นที่ที่ดูสวยงามและเนื้อละเอียดได้อย่างลงตัว เป็นเหตุผลที่ในตัวอาหารท้องถิ่นนั้นใช้ศาสตร์ของรูปภาพวงกลมในการปรับปรุงสูตรอาหารอีกด้วย
นอกจากการใช้อย่างประจักษ์ในชีวิตประจำวันแล้ว รูปภาพวงกลมยังมีคำถามที่พบบ่อยในประเด็นนี้ ดังต่อไปนี้:
คำถามที่ 1: วงกลมไม่ใช่รูปทรงที่เกิดได้อย่างธรรมชาติจากอะไร?
คำตอบ: วงกลมเป็นรูปทรงที่ไม่เกิดจากธรรมชาติแต่เป็นผลลัพธ์จากการวาดเส้นและการแปลงร่างของวัตถุทางศิลปะและคณิตศาสตร์
คำถามที่ 2: รูปภาพวงกลมมีคุณสมบัติเฉพาะใดบ้าง?
คำตอบ: รูปภาพวงกลมมีคุณสมบัติเฉพาะ 2 คุณสมบัติ คือ (1) รัศมีของวงกลมเป็นค่าคงที่ และ (2) รูปภาพวงกลมมีจุดศูนย์กลางที่เป็นจุดตรงกลางของวงกลม
คำถามที่ 3: วงกลมทำงานร่วมกับรูปร่างอื่น ๆ ได้อย่างไร?
คำตอบ: วงกลมสามารถทำงานร่วมกับรูปร่างอื่น ๆ ได้อย่างหลายวิธี เช่น อาจเป็นรูปร่างหุนยนต์ที่มีลักษณะราวกับวงกลมหรือเป็นวัตถุที่เหมือนสัญลักษณ์เดียวกัน เนื่องจากรูปภาพวงกลมมีความง่ายและละเอียดอ่อนด้วยตัวเอง นอกจากนี้ยังมีรูปภาพวงกลมบรรดานกับรูปร่างอื่น ๆ ที่สร้างเส้นรอบรูปร่างนั้น ๆ
หวังว่าบทความนี้จะให้คุณเห็นถึงความสำคัญและการใช้งานของรูปภาพวงกลมในชีวิตประจำวัน ไม่ว่าจะเป็นในทางทฤษฎีทางคณิตศาสตร์ กราฟิกดีไซน์ ใช้ในวาดและเขียน หรือแม้กระทั่งการใช้อย่างง่ายดายในการทำอาหาร รูปภาพวงกลมเป็นสัญลักษณ์ที่ดีที่สุดในการหาคำตอบในเรื่องการออกแบบและแก้ปัญหาในชีวิตประจำวันของเรา
สามเหลี่ยมภาษาอังกฤษ
สามเหลี่ยมเป็นรูปหนึ่งที่มีสามเส้นขอบและสามมุม ภาษาอังกฤษมีคำศัพท์และอธิบายสำหรับสามเหลี่ยมที่ช่วยให้เราสามารถอธิบายและเข้าใจรูปร่างของสามเหลี่ยมได้อย่างถูกต้องและเหมาะสม ในบทความนี้เราจะพิจารณาถึงคำศัพท์ที่เกี่ยวข้องกับสามเหลี่ยมในภาษาอังกฤษและวิธีการใช้คำศัพท์นี้ในบริบทที่แตกต่างกันไป นอกจากนี้ยังจะมีส่วนถามตอบที่พบบ่อยที่สุดเกี่ยวกับสามเหลี่ยมเพื่อให้คุณได้อ่านและเรียนรู้เพิ่มเติมเกี่ยวกับกระแสการใช้ภาษาอังกฤษในแนวคิดของสามเหลี่ยม
คำศัพท์ที่เกี่ยวข้องกับสามเหลี่ยมในภาษาอังกฤษ
1. Triangle (n.) – สามเหลี่ยม
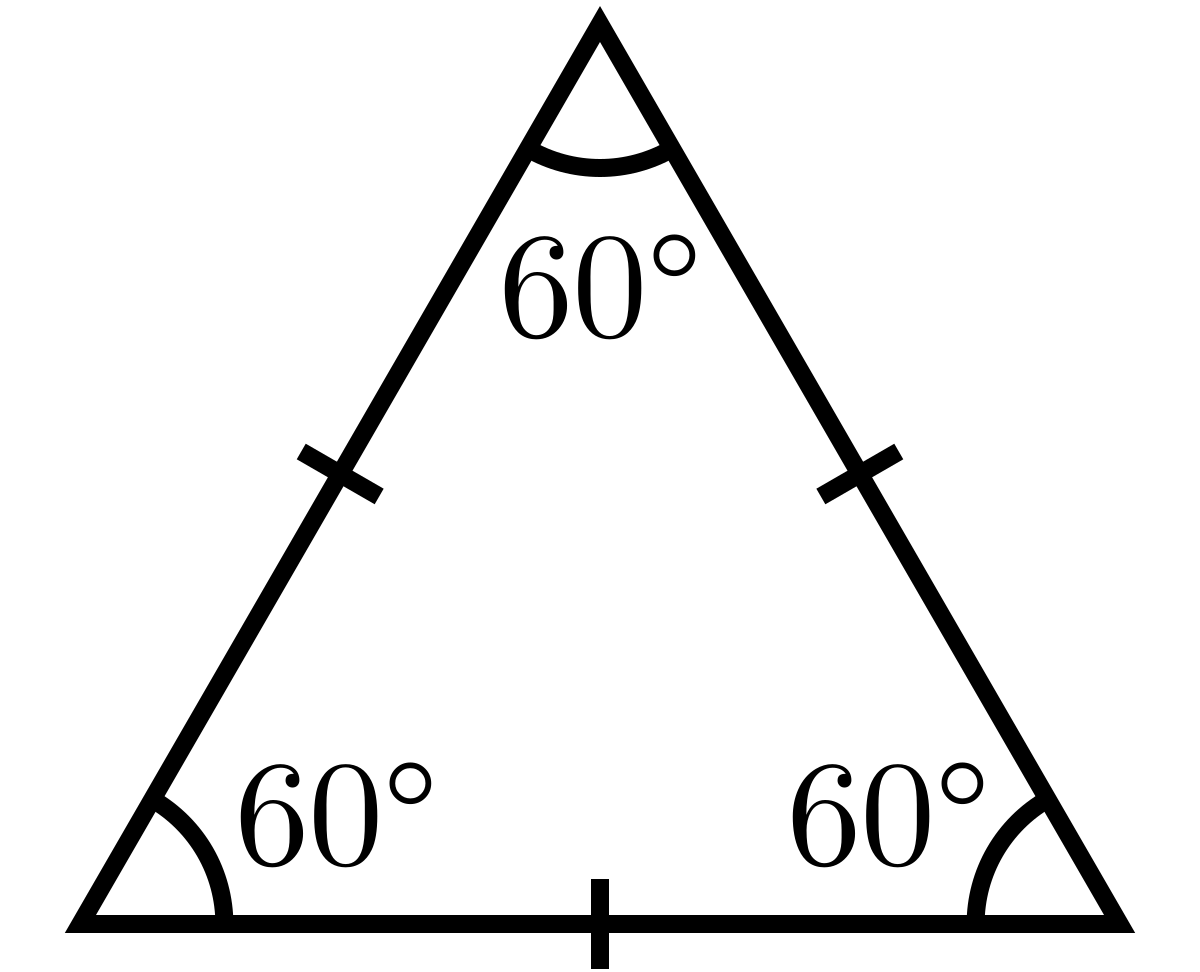
2. Equilateral triangle (n.) – สามเหลี่ยมด้านเท่า
3. Isosceles triangle (n.) – สามเหลี่ยมปานกลาง
4. Scalene triangle (n.) – สามเหลี่ยมที่ด้านไม่เท่ากัน
5. Right triangle (n.) – สามเหลี่ยมมุมฉาก
6. Acute triangle (n.) – สามเหลี่ยมมุมคม
7. Obtuse triangle (n.) – สามเหลี่ยมมุมป้าน
8. Base (n.) – ฐาน
9. Height (n.) – สูง
10. Vertex (n.) – จุดยอด
11. Perimeter (n.) – เส้นรอบรูป
12. Area (n.) – พื้นที่
13. Hypotenuse (n.) – ด้านตรงข้ามมุมฉาก
การใช้คำศัพท์ที่เกี่ยวข้องกับสามเหลี่ยมในบริบทที่แตกต่างกัน
1.คำศัพท์สามเหลี่ยม
– I drew a triangle on the whiteboard. (ฉันวาดรูปสามเหลี่ยมบนกระดานขาว)
– The triangle has three sides and three angles. (สามเหลี่ยมมีด้านสามด้านและมุมสามมุม)
2.คำศัพท์ในเชิง meet
– The two sides of the triangle meet at a point. (ด้านสองด้านของสามเหลี่ยมพบกันที่จุดหนึ่ง)
– The lines intersected and formed a triangle. (เส้นสองอันตัดกันและเป็นรูปสามเหลี่ยม)
3.คำศัพท์ในบริบททางคณิตศาสตร์
– We studied the properties of different types of triangles. (เราศึกษาคุณสมบัติของสามเหลี่ยมประเภทต่าง ๆ)
– The theorem states that the sum of the angles in a triangle is 180 degrees. (ทฤษฎีกล่าวไว้ว่าผลบวกของมุมในสามเหลี่ยมเป็น 180 องศา)
4.คำศัพท์ในเชิง meet
– The two sides of the triangle meet at a point. (ด้านสองด้านของสามเหลี่ยมพบกันที่จุดหนึ่ง)
– The lines intersected and formed a triangle. (เส้นสองอันตัดกันและเป็นรูปสามเหลี่ยม)
ส่วนถามตอบเกี่ยวกับสามเหลี่ยมที่พบบ่อยที่สุด
1. สามเหลี่ยมเท่ากันคืออะไร?
สามเหลี่ยมเท่ากันหมายถึงสามเหลี่ยมที่มีทั้งสามด้านและสามมุมเท่ากัน ดังนั้น, หากมีสามด้านที่มีความยาวเท่ากันและสามมุมที่มีมุมอัตราศัพท์เท่ากัน แล้วสามเหลี่ยมนั้นจะถือว่าเป็นสามเหลี่ยมเท่ากัน
2. สามเหลี่ยมมุมฉากคืออะไร?
สามเหลี่ยมมุมฉากเป็นสามเหลี่ยมที่มีหนึ่งมุมมุมฉากซึ่งหมายความว่ามุมนั้นมีอัตราศัพท์มากกว่า 90 องศา สามเหลี่ยมมุมฉากใช้กับอากรูพิจารณาเชิงสถิติและมีหลายประยุกต์ในการแก้ปัญหาทางคณิตศาสตร์และระบบเรียนการศึกษา
3. สามเหลี่ยมมุมคมคืออะไร?
สามเหลี่ยมมุมคมเป็นสามเหลี่ยมที่มีทุกมุมมุมที่มีอัตราศัพท์มากกว่า 0 องศาและน้อยกว่า 90 องศา สามเหลี่ยมมุมคมมักใช้ในคณิตศาสตร์เพื่ออธิบายรูปร่างของเกมหรือหลายอย่างที่เกี่ยวข้องกับอัตราส่วนที่เล็กที่สุด
4. สามเหลี่ยมมุมป้านคืออะไร?
สามเหลี่ยมมุมป้านเป็นสามเหลี่ยมที่มีหนึ่งมุมมุมที่มีค่ามากกว่า 90 องศา แต่น้อยกว่า 180 องศา สามเหลี่ยมมุมป้านสามารถใช้ในงานวิจัยคณิตศาสตร์หรืองานอื่น ๆ ที่มีความต้องการต้องการอธิบายรูปร่างที่ไม่ได้มีอัตราส่วนธรรมดาหลัก
5. สามเหลี่ยมรูปใดที่ใช้คำว่าฐานและสูง?
สามเหลี่ยมประเภทใดก็ตามที่มีฐานและสูงซึ่งเป็นคุณลักษณะของรูปร่างตามที่อธิบายไว้ สามเหลี่ยมที่มีฐานและสูงมีเกี่ยวข้องกับการคำนวณพื้นที่ของสามเหลี่ยม ความยาวเส้นฐานนับเป็นพารามิเตอร์สามารถใช้เพื่อคำนวณพื้นที่ของรูปสามเหลี่ยมได้
แน่ใจว่าคุณเข้าใจและทราบเกี่ยวกับคำศัพท์และคุณลักษณะพื้นฐานของสามเหลี่ยมภาษาอังกฤษแล้วมากยิ่งขึ้นกัน หวังว่าบทความนี้จะช่วยให้คุณเข้าใจเกี่ยวกับรูปร่างและคุณลักษณะของสามเหลี่ยมเพิ่มขึ้น และสามารถนำความรู้นี้ไปใช้ในการศึกษาเพิ่มเติมอีกด้วย
คำถามที่พบบ่อย (FAQs)
Q: สามเหลี่ยมมุมฉากและสามเหลี่ยมมุมป้านเหมือนกันหรือไม่?
A: ไม่ เพราะสามเหลี่ยมมุมฉากมีมุมที่เป็นศูนย์กลางที่มุมมุมฉากเท่ากับ 90 องศา ในขณะที่สามเหลี่ยมมุมป้านมีมุมที่มีค่ามากกว่า 90 องศาแต่น้อยกว่า 180 องศา
Q: สามเหลี่ยมอาจเป็นสี่เหลี่ยมได้หรือไม่?
A: ไม่ได้ เพราะสามเหลี่ยมมีสามด้าน ในขณะที่สี่เหลี่ยมมีสี่ด้าน
Q: สามเหลี่ยมมีกี่ชนิด?
A: สามเหลี่ยมมีสามชนิดหลัก คือ สามเหลี่ยมด้านเท่า (equilateral triangle), สามเหลี่ยมปานกลาง (isosceles triangle), และสามเหลี่ยมที่ด้านไม่เท่ากัน (scalene triangle)
Q: สามเหลี่ยมมุมคมเป็นสามเหลี่ยมด้านเท่าหรือไม่?
A: ไม่ใช่ เพราะสามเหลี่ยมมุมคมไม่มีทั้งสามด้านที่เท่ากัน
Q: สามเหลี่ยมมุมฉากใช้ทางไหนในชีวิตประจำวัน?
A: สามเหลี่ยมมุมฉากมีการประยุกต์ใช้ในงานก่อสร้าง, การวาดแผนผัง, การแก้ไขปัญหาทางคณิตศาสตร์และหลายแนวทางอื่นในชีวิตประจำวัน
มี 12 ภาพที่เกี่ยวข้องกับหัวข้อ สามเหลี่ยม สี่เหลี่ยม วงกลม.

















![ลักษณะของรูปสามเหลี่ยม รูปสี่เหลี่ยม วงกลม และวงรี [ Learn with Socrates ] - YouTube ลักษณะของรูปสามเหลี่ยม รูปสี่เหลี่ยม วงกลม และวงรี [ Learn With Socrates ] - Youtube](https://i.ytimg.com/vi/YK6FX3KX3DI/hqdefault.jpg)



![tutustory 图图是道] [[ รูปทรงเรขาคณิตภาษาจีนเรียกยังไงนะ? | รูปร่างและรูปทรงในภาษาจีน 形状 ]] #เนื้อหาภาษาจีน #รูปทรงภาษาจีน #สร้างภาพเล่าเรื่อง #图图是道 Tutustory 图图是道] [[ รูปทรงเรขาคณิตภาษาจีนเรียกยังไงนะ? | รูปร่างและรูปทรงในภาษาจีน 形状 ]] #เนื้อหาภาษาจีน #รูปทรงภาษาจีน #สร้างภาพเล่าเรื่อง #图图是道](https://t1.blockdit.com/photos/2021/06/60bc9691deff370c786008fb_800x0xcover_Gg5cMUaA.jpg)














ลิงค์บทความ: สามเหลี่ยม สี่เหลี่ยม วงกลม.
ดูข้อมูลเพิ่มเติมเกี่ยวกับโพสต์หัวข้อนี้ สามเหลี่ยม สี่เหลี่ยม วงกลม.
- สามเหลี่ยม สี่เหลี่ยม วงกลม จาก Squid Game จนถึงโลกศิลปะ
- เรื่อง รูปสามเหลี่ยม รูปสี่เหลี่ยม รูปวงกลม และวงรี – DLTV
- การเขียนรูปสามเหลี่ยม รูปสี่เหลี่ยม วงกลม และวงรีโดยใช้แบบของรูป
- Psychology of Shapes – จิตวิทยารูปทรงและรูปร่าง ดีไซน์สื่อนัยยะ
- การเรียนรู้สี่เหลี่ยม สามเหลี่ยม วงกลมสีเหลือง – Kids and Toys
ดูเพิ่มเติม: https://buoitutrung.com/news/