Tìm thấy 24 bài viết phù hợp với toán hình 11 bài 7.










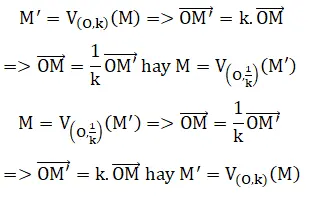




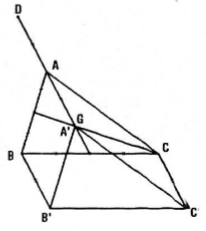

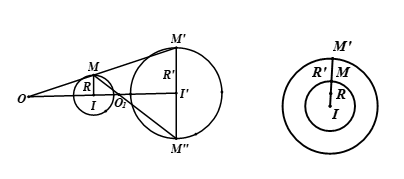
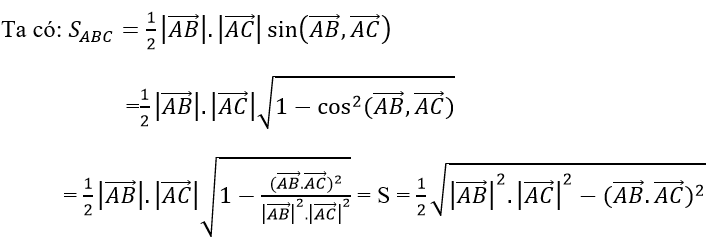

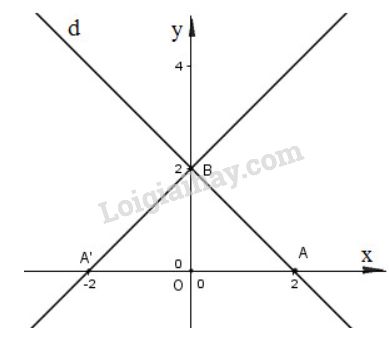










toán hình 11 bài 7
Toán hình 11 bài 7 là một bài toán trong chương trình hình học không gian của lớp 11. Bài toán này liên quan đến vị trí tương đối giữa một đường thẳng và một mặt phẳng trong không gian. Để giải quyết bài toán này, cần phải nắm vững các kiến thức cơ bản về hình học không gian cũng như tính chất của các đường thẳng, mặt phẳng đặc biệt trong không gian.
I. Khái niệm về hình học không gian
1. Tổng quan về hình học không gian:
Hình học không gian là một phần của hình học, nghiên cứu về các đối tượng không gian như các hình khối, các đường thẳng, mặt phẳng, … trong không gian. Hình học không gian đã có ứng dụng trong nhiều lĩnh vực như kỹ thuật, kiến trúc, chỉ số tài chính, giải trí, …
2. Định nghĩa đối tượng trong hình học không gian:
– Đường thẳng trong không gian là tập hợp các điểm liên tiếp và không có điểm chung với một mặt phẳng.
– Mặt phẳng trong không gian là tập hợp các điểm phẳng trong không gian mà bất kỳ hai điểm nào của mặt phẳng đó đều có thể vẽ được một đoạn thẳng nằm trên mặt phẳng đó.
– Hình khối trong không gian là tập hợp các điểm trong không gian được bao quanh bởi các mặt phẳng hoặc các đường thẳng.
3. Khác biệt giữa hình học không gian và hình học phẳng:
– Hình học không gian: Nghiên cứu về các đối tượng trong ba chiều (độ dài, độ rộng, độ cao).
– Hình học phẳng: Nghiên cứu về các đối tượng trong hai chiều (độ dài, độ rộng).
II. Khái niệm về vị trí tương đối giữa hai mặt phẳng trong không gian
1. Định nghĩa vị trí tương đối giữa hai mặt phẳng:
Vị trí tương đối giữa hai mặt phẳng trong không gian có các trường hợp sau:
– Hai mặt phẳng trùng nhau.
– Hai mặt phẳng song song.
– Hai mặt phẳng cắt nhau tạo thành một đường thẳng.
– Hai mặt phẳng cắt nhau.
2. Các trường hợp vị trí tương đối giữa hai mặt phẳng:
– Hai mặt phẳng trùng nhau: tức là hai mặt phẳng này hoàn toàn giống nhau và có các điểm chung.
– Hai mặt phẳng song song: tức là hai mặt phẳng không có điểm chung giao nhau.
– Hai mặt phẳng cắt nhau tạo thành một đường thẳng: đường thẳng giao của hai mặt phẳng này là duy nhất.
– Hai mặt phẳng cắt nhau: tức là hai mặt phẳng này giao nhau tạo thành một đường thẳng.
3. Ý nghĩa của việc tìm hiểu vị trí tương đối giữa hai mặt phẳng:
Vị trí tương đối giữa hai mặt phẳng là một kiến thức cơ bản và quan trọng trong hình học không gian. Nó giúp ta hiểu được các tính chất của các đơn vị hình học khác nhau và giải quyết các bài toán liên quan đến hình học không gian.
III. Các đường thẳng, mặt phẳng đặc biệt trong không gian
1. Đường thẳng vuông góc với một mặt phẳng:
Đường thẳng vuông góc với một mặt phẳng là đường thẳng mà nằm trên mặt phẳng vuông góc với mặt phẳng đó.
2. Mặt phẳng vuông góc với một đường thẳng:
Mặt phẳng vuông góc với một đường thẳng là mặt phẳng mà nằm trên đường thẳng đó và vuông góc với đường thẳng đó.
3. Các đường thẳng, mặt phẳng đặc biệt trong các hình khối:
– Hình hộp chữ nhật: Các cạnh của hình hộp vuông góc với nhau.
– Hình lăng trụ đứng: Các cạnh của hình lăng trụ vuông góc với đáy.
– Hình lăng trụ nghiêng: Các cạnh của hình lăng trụ không vuông góc với đáy.
IV. Tính chất của hình lập phương và hình chóp cụt đáy vuông
1. Định nghĩa hình lập phương và hình chóp cụt đáy vuông:
– Hình lập phương: là một hình khối có 6 mặt phẳng, mỗi mặt phẳng đều là hình vuông và cạnh của hình vuông bằng nhau.
– Hình chóp cụt đáy vuông: là hình khối có 2 mặt phẳng, một mặt phẳng là hình vuông, và mặt phẳng kia là một hình bất kỳ.
2. Các tính chất của hình lập phương và hình chóp cụt đáy vuông:
– Thể tích của hình lập phương là a^3.
– Thể tích của hình chóp cụt đáy vuông là (1/3) x SĐ x h, trong đó SĐ là diện tích đáy, h là chiều cao của hình chóp.
3. Ứng dụng của hình lập phương và hình chóp cụt đáy vuông trong thực tế:
Hình lập phương và hình chóp cụt đáy vuông được ứng dụng trong nhiều lĩnh vực như kiến trúc, kỹ thuật, thiết kế, xây dựng, vật liệu xây dựng, …
V. Các bài toán liên quan đến không gian
1. Hình học giải tích trong không gian:
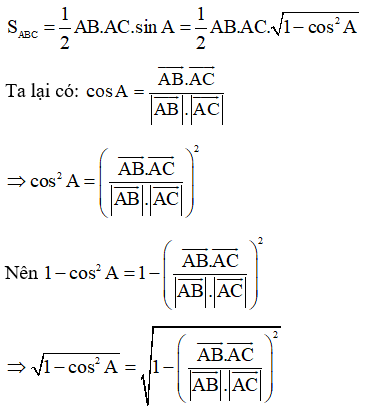
Hình học giải tích là một phương pháp để giải quyết các bài toán hình học bằng cách sử dụng các công thức toán học.
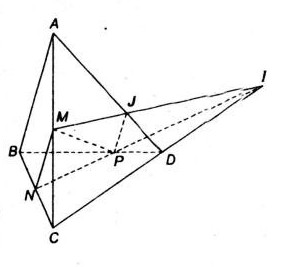
2. Bài toán xác định vị trí tương đối của một đường thẳng và một mặt phẳng:
Bài toán này yêu cầu tìm vị trí tương đối của một đường thẳng và một mặt phẳng trong không gian.
3. Bài toán tính thể tích của hình lập phương và hình chóp cụt đáy vuông:
Bài toán này yêu cầu tính toán thể tích của hình lập phương và hình chóp cụt đáy vuông.
FAQs:
1. Hình khối là gì?
Hình khối là một đối tượng trong không gian được bao quanh bởi các mặt phẳng hoặc các đường thẳng.
2. Định nghĩa của mặt phẳng vuông góc với một đường thẳng?
Mặt phẳng vuông góc với một đường thẳng là mặt phẳng mà nằm trên đường thẳng đó và vuông góc với đường thẳng đó.
3. Thể tích của hình lập phương là bao nhiêu?
Thể tích của hình lập phương là a^3, trong đó a là cạnh của hình vuông.
4. Cách tính thể tích của hình chóp cụt đáy vuông là gì?
Thể tích của hình chóp cụt đáy vuông là (1/3) x SĐ x h, trong đó SĐ là diện tích đáy, h là chiều cao của hình chóp.
Từ khoá người dùng tìm kiếm: toán hình 11 bài 7 Toán hình 11 Bài 7 lý thuyết, Toán hình 11 Bài 8, Toán Hình 11 Bài 8 phép đồng dạng, Toán 11 phép vị tự Lý thuyết, Toán 11 Bài 8, Bài 7 Toán Hình 11 trang 54, Toán 11 phép đồng dạng, Bài tập phép vị tự có đáp an
Tag: Album 22 – toán hình 11 bài 7
Phép vị tự – Bài 7 – Toán học 11 – Thầy Lê Thành Đạt (DỄ HIỂU NHẤT)
Xem thêm tại đây: buoitutrung.com
Link bài viết: toán hình 11 bài 7.
Xem thêm thông tin về chủ đề toán hình 11 bài 7.
- Giải Toán 11 Bài 7: Phép vị tự – VietJack.com
- Phép Vị Tự – Toán 11 – Loigiaihay.com
- Sách Giải Bài Tập Toán Lớp 11 Bài 7: Phép Vị Tự
- Giải toán 11 Bài 7. Phép vị tự
- Hình học 11 Bài 7: Phép vị tự – HOC247
- Soạn hình học 11 bài 7: Phép vị tự | Học cùng hocthoi.net
- Giải bài tập Bài 7: Phép vị tự – SGK Hình học lớp 11
- Giải Toán 11: Bài 7 trang 120 SGK Hình học 11 – Toploigiai
Categories: https://buoitutrung.com/img/
